Diferenças entre edições de "Distribuição normal"

Revisão das 19h17min de 16 de novembro de 2007

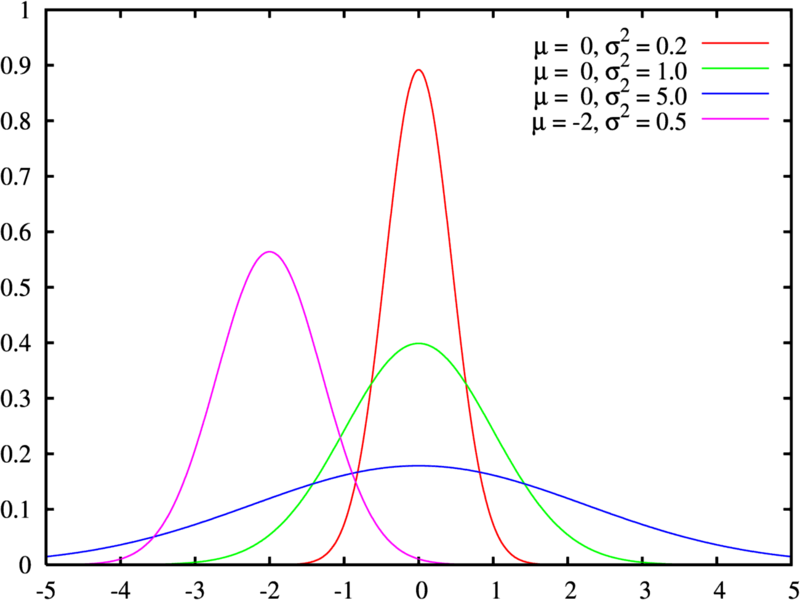A distribuição normal é a distribuição de probabilidade mais frequente em estatística. Foi desenvolvida pelo matemático francês Abraham de Moivre. As suas características fundamentais são a média e o desvio padrão.

Função de densidade de probabilidade

A função densidade de probabilidade da distribuição normal com média $\mu$ e variância $\sigma^2$ (de forma equivalente, desvio padrão $\sigma$ ) é assim definida,

$f(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right).$

Se a variável aleatória $X$ segue esta distribuição escreve-se: $X$ ~ $N(\mu, \sigma^2)$ .

Se $\mu = 0$ e $\sigma = 1$ , a distribuição é chamada de distribuição normal padrão e a função de densidade de probabilidade reduz-se a,

$f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right).$

Propriedades

Se X segue uma distribuição normal, então a X + b também segue.
Se X e Y são distribuições normais, então sua soma U = X + Y e diferença V = X - Y também são distribuições normais.
- Se X e Y são independentes, então U e V também serão independentes.
A soma de uma grande quantidade de variáveis aleatórias (com algumas restrições) tende a uma distribuição normal - o significado mais preciso disto é o Teorema do Limite Central.
A distribuição normal é infinitamente divisível, no seguinte sentido: se X é uma variável aleatória que segue uma distribuição normal e n é um número natural, então existem n variáveis aletórias $X_1, X_2, \ldots X_n\,$ , independentes e identicamente distribuídas, tal que

$X = X_1 + X_2 + \ldots + X_n\,$

Distribuições relacionadas

$R \sim \mathrm{Rayleigh}(\sigma^2)$ é a distribuição de Rayleigh se $R = \sqrt{X^2 + Y^2}$ onde $X \sim N(0, \sigma^2)$ e $Y \sim N(0, \sigma^2)$ são duas distribuições normais independentes.
$Y \sim \chi_{\nu}^2$ é a distribuição Chi-quadrado com $\nu$ graus de liberdade se $Y = \sum_{k=1}^{\nu} X_k^2$ em que $X_k \sim N(0,1)$ para $k=0,1,\cdots,\nu$ são distribuições normais padrão independentes.
$Y \sim \mathrm{Cauchy}(\mu = 0, \theta = 1)$ é a distribuição de Cauchy se $Y = X_1/X_2$ para $X_1 \sim N(0,1)$ e $X_2 \sim N(0,1)$ são duas distribuições normais padrão independentes.
$Y \sim \mbox{Log-N}(\mu, \sigma^2)$ é a distribuição log-normal se $Y = e^X$ e $X \sim N(\mu, \sigma^2)$ .
Relação com Lévy skew alpha-stable distribution: se $X\sim \textrm{Levy-S}\alpha\textrm{S}(2,\beta,\sigma/\sqrt{2},\mu)$ então $X \sim N(\mu,\sigma^2)$ .
Distribuição normal truncada: Se $X \sim N(\mu, \sigma^2)$ então, truncando para valores entre $A$ e $B$ temos uma variável aleatória contínua com média $E(X)=\mu + \frac{\sigma(\phi_1-\phi_2)}{T}$ , em que $T=\Phi\left(\frac{B-\mu}{\sigma}\right)-\Phi\left(\frac{A-\mu}{\sigma}\right)$ , $\phi_1=f\left(\frac{A-\mu}{\sigma}\right)$ e $\phi_2=f\left(\frac{B-\mu}{\sigma}\right)$ , sendo $f(\cdot)$ a função densidade de probabilidade e $\Phi(\cdot)$ a função de probabilidade acumulada de uma distribuição normal padrão.

Simulação

Implementações computacionais do Método de Monte Carlo normalmente precisam simular várias variáveis aleatórias normais. Muitos programas e pacotes não conseguem simular diretamente a normal, mas tem simuladores da distribuição uniforme. Uma forma rápida e prática de gerar normais a partir da uniforme é a transformação de Box-Muller: sejam $U_1$ e $U_2$ valores independentes gerados pela distribuição uniforme entre 0 e 1. Então:

$Z_1 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)\,$

e

$Z_2 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2).\,$

são normais padronizadas independentes.

Esta página usa conteúdo da Wikipedia. O artigo original estava em Curva normal. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License.

@@ Linha 2: / Linha 2: @@
 A '''distribuição normal''' é a distribuição de probabilidade mais frequente em estatística. Foi desenvolvida pelo matemático francês Abraham de Moivre. As suas características fundamentais são a média e o desvio padrão.
-=== Função de densidade de probabilidade ===
+==Função de densidade de probabilidade==
 A [[função densidade de probabilidade]] da '''distribuição normal''' com [[média]] <tex>\mu</tex> e [[variância]] <tex>\sigma^2</tex> (de forma equivalente, [[desvio padrão]] <tex>\sigma</tex>) é assim definida,
@@ Linha 18: / Linha 18: @@
-== Propriedades ==
+==Propriedades==
 * Se ''X'' segue uma distribuição normal, então ''a X + b'' também segue.
 * Se ''X'' e ''Y'' são distribuições normais, então sua soma ''U = X + Y'' e diferença ''V = X - Y'' também são distribuições normais.
@@ Linha 27: / Linha 27: @@
-== Distribuições relacionadas  ==
+==Distribuições relacionadas ==
 *<tex>R \sim \mathrm{Rayleigh}(\sigma^2)</tex> é a [[distribuição de Rayleigh]] se <tex>R = \sqrt{X^2 + Y^2}</tex> onde <tex>X \sim N(0, \sigma^2)</tex> e <tex>Y \sim N(0, \sigma^2)</tex> são duas distribuições normais independentes.
 *<tex>Y \sim \chi_{\nu}^2</tex> é a [[distribuição Chi-quadrado]] com <tex>\nu</tex> [[graus de liberdade]] se <tex>Y = \sum_{k=1}^{\nu} X_k^2</tex> em que <tex>X_k \sim N(0,1)</tex> para <tex>k=0,1,\cdots,\nu</tex> são distribuições normais padrão independentes.
@@ Linha 36: / Linha 36: @@
-== Simulação ==
+==Simulação==
 Implementações computacionais do [[Método de Monte Carlo]] normalmente precisam simular várias variáveis aleatórias normais. Muitos programas e pacotes não conseguem simular diretamente a normal, mas tem simuladores da [[distribuição uniforme]]. Uma forma rápida e prática de gerar normais a partir da uniforme é a [[transformação de Box-Muller]]: sejam <tex>U_1</tex> e <tex>U_2</tex> valores independentes gerados pela distribuição uniforme entre 0 e 1. Então:

Diferenças entre edições de "Distribuição normal"

Revisão das 19h17min de 16 de novembro de 2007

Índice

Função de densidade de probabilidade

Propriedades

Distribuições relacionadas

Simulação

Menu de navegação

Vistas

Ferramentas pessoais

Navegação

Pesquisa

Ferramentas