Distribuição normal

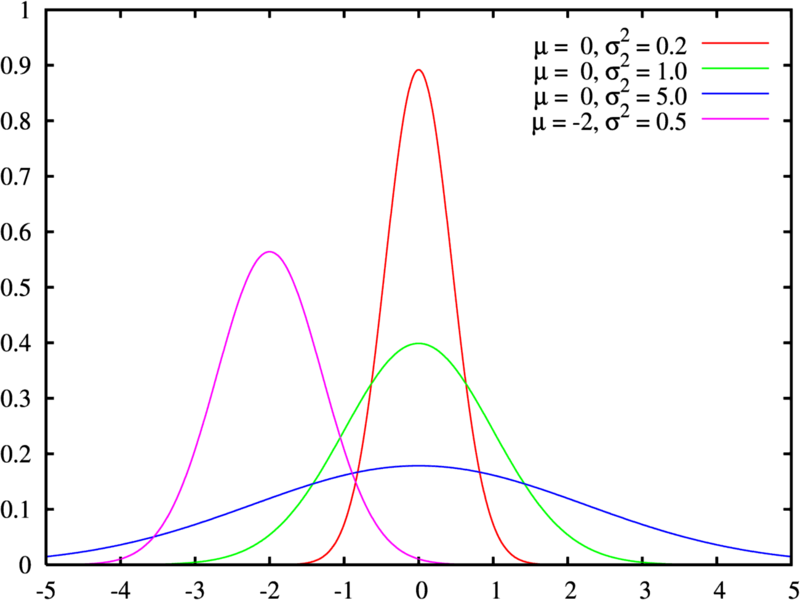A distribuição normal é a distribuição de probabilidade mais frequente em estatística. Foi desenvolvida pelo matemático francês Abraham de Moivre. As suas características fundamentais são a média e o desvio padrão.

Índice

1 Função de densidade de probabilidade
2 Propriedades
3 Distribuições relacionadas
4 Simulação

Função de densidade de probabilidade

A função densidade de probabilidade da distribuição normal com média $\mu$ e variância $\sigma^2$ (de forma equivalente, desvio padrão $\sigma$ ) é assim definida,

$f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right).$

Se a variável aleatória $X$ segue esta distribuição escreve-se:

$X$ ~ $N(\mu, \sigma^2)$ .

Se $\mu = 0$ e $\sigma = 1$ , a distribuição é chamada de distribuição normal padrão e a função de densidade de probabilidade reduz-se a,

$f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right).$

Propriedades

Se X segue uma distribuição normal, então a X + b também segue.
Se X e Y são distribuições normais, então sua soma U = X + Y e diferença V = X - Y também são distribuições normais.
- Se X e Y são independentes, então U e V também serão independentes.
A soma de uma grande quantidade de variáveis aleatórias (com algumas restrições) tende a uma distribuição normal - o significado mais preciso disto é o Teorema do Limite Central.
A distribuição normal é infinitamente divisível, no seguinte sentido: se X é uma variável aleatória que segue uma distribuição normal e n é um número natural, então existem n variáveis aletórias $X_1, X_2, \ldots X_n\,$ , independentes e identicamente distribuídas, tal que

$X = X_1 + X_2 + \ldots + X_n\,$

Distribuições relacionadas

$R \sim \mathrm{Rayleigh}(\sigma^2)$ é a distribuição de Rayleigh se $R = \sqrt{X^2 + Y^2}$ onde $X \sim N(0, \sigma^2)$ e $Y \sim N(0, \sigma^2)$ são duas distribuições normais independentes.

$Y \sim \chi_{\nu}^2$ é a distribuição Chi-quadrado com $\nu$ graus de liberdade se $Y = \sum_{k=1}^{\nu} X_k^2$ em que $X_k \sim N(0,1)$ para $k=0,1,\cdots,\nu$ são distribuições normais padrão independentes.

$Y \sim \mathrm{Cauchy}(\mu = 0, \theta = 1)$ é a distribuição de Cauchy se $Y = X_1/X_2$ para $X_1 \sim N(0,1)$ e $X_2 \sim N(0,1)$ são duas distribuições normais padrão independentes.

$Y \sim \mbox{Log-N}(\mu, \sigma^2)$ é a distribuição log-normal se $Y = e^X$ e $X \sim N(\mu, \sigma^2)$ .

Relação com distribuição Lévy skew alpha-stable: se $X\sim \textrm{Levy-S}\alpha\textrm{S}(2,\beta,\sigma/\sqrt{2},\mu)$ então $X \sim N(\mu,\sigma^2)$ .

Distribuição normal truncada: Se $X \sim N(\mu, \sigma^2)$ então, truncando para valores entre $A$ e $B$ temos uma variável aleatória contínua com média $E(X)=\mu + \frac{\sigma(\phi_1-\phi_2)}{T}$ , em que $T=\Phi\left(\frac{B-\mu}{\sigma}\right)-\Phi\left(\frac{A-\mu}{\sigma}\right)$ , $\phi_1=f\left(\frac{A-\mu}{\sigma}\right)$ e $\phi_2=f\left(\frac{B-\mu}{\sigma}\right)$ , sendo $f(\cdot)$ a função densidade de probabilidade e $\Phi(\cdot)$ a função de probabilidade acumulada de uma distribuição normal padrão.

Simulação

Implementações computacionais do Método de Monte Carlo normalmente precisam simular várias variáveis aleatórias normais. Muitos programas e pacotes não conseguem simular diretamente a normal, mas tem simuladores da distribuição uniforme. Uma forma rápida e prática de gerar normais a partir da uniforme é a transformação de Box-Muller: sejam $U_1$ e $U_2$ valores independentes gerados pela distribuição uniforme entre 0 e 1. Então:

$Z_1 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)\,$

e

$Z_2 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2).\,$

são normais padronizadas independentes.

Esta página usa conteúdo da Wikipedia. O artigo original estava em Distribuição normal. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License.

Distribuição normal

Índice

Função de densidade de probabilidade

Propriedades

Distribuições relacionadas

Simulação

Menu de navegação

Vistas

Ferramentas pessoais

Navegação

Pesquisa

Ferramentas