Diferenças entre edições de "Correlação"

Da Thinkfn
(→‎Propriedades matemáticas)
 
(6 edições intermédias não estão a ser mostradas.)
Linha 1: Linha 1:
−
Em teoria da probabilidade e [[estatística]], '''correlação''', também chamada de '''coeficiente de correlação''', indica a força e a direcção do relacionamento linear entre duas [[variável aleatória|variáveis aleatórias]]. No uso estatístico geral, ''correlação'' ou co-relação se refere a medida da relação entre duas variáveis, embora correlação não implique [[causalidade]]. Neste sentido geral, existem vários coeficientes medindo o grau de correlação, adaptados à natureza dos dados.
+
<metadesc content="Na teoria das probabilidades e na estatística, correlação (frequentemente medida na forma de um coeficiente de correlação) indica a força e a direcção da relação linear entre duas variáveis aleatórias." />
  
−
Vários coeficientes são utilizados para situações diferentes. O mais conhecido é o [[coeficiente de correlação de Pearson]], o qual é obtido dividindo a [[covariância]] de duas variáveis pelo produto de seus [[desvio padrão|desvios padrão]]. Apesar do nome, ela foi apresentada inicialmente por [[Francis Galton]].
+
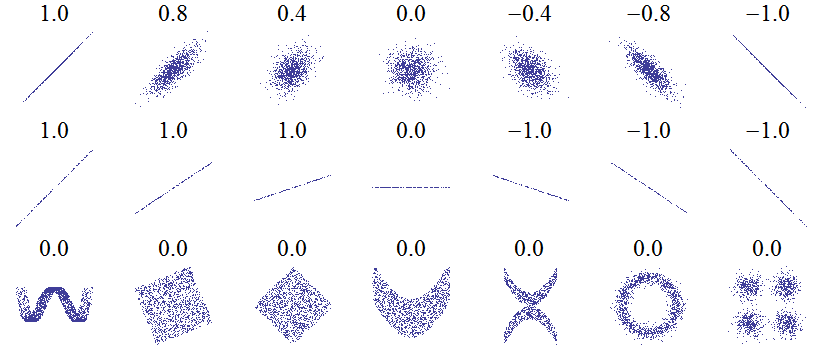
[[Imagem:ExemplosCorrelacao.png|thumb|400px|right|Diagramas de dispersão de pontos (''x'',&nbsp;''y''), com o coeficiente de ''x'' e ''y'' para cada conjunto. Note que a correlação reflecte o ruído e a direcção de uma relação ''linear'' (na primeira linha), mas não a inclinação dessa relação (linha do meio), nem muitos outros aspectos das relações não-lineares (última linha). N.B.: a figura central tem uma inclinação zero mas neste caso o coeficiente de correlação é indefinido porque a [[variância]] de ''y'' é zero.]]
  
 +
Na [[teoria das probabilidades]] e na [[estatística]], '''correlação''' (frequentemente medida na forma de um '''coeficiente de correlação''') indica a força e a direcção da relação ''linear'' entre duas [[variável aleatória|variáveis aleatórias]]. Esta definição difere do uso normal do termo correlação, que se refere a qualquer relação, não necessariamente linear.
 +
 +
No uso geral em estatística, ''correlação'' refere-se à medida em que duas variáveis aleatórias se afastam da [[independência estatística]]. Neste sentido geral, existem vários coeficientes para medir o grau de correlação, adaptados à natureza dos dados.
  
 
==Coeficiente produto-momento de Pearson==
 
==Coeficiente produto-momento de Pearson==
 +
Vários coeficientes são utilizados para situações diferentes. O mais conhecido é o [[coeficiente de correlação de Pearson]], o qual é obtido dividindo a [[covariância]] de duas variáveis pelo produto dos seus [[desvio padrão|desvios padrão]]. Apesar do nome, ela foi inicialmente apresentada por Francis Galton<ref name="13ways">
 +
{{Cite journal
 +
| last = Rodgers
 +
| first = J. L.
 +
| coauthors = Nicewander, W. A.
 +
| title = Thirteen ways to look at the correlation coefficient
 +
| journal = The American Statistician
 +
| year = 1988
 +
| volume = 42
 +
| pages = 59–66
 +
| language = en
 +
| doi = 10.2307/2685263
 +
}}
 +
</ref>.
 +
 
=== Propriedades matemáticas ===
 
=== Propriedades matemáticas ===
−
O coeficiente de correlação &rho;<sub>''X, Y''</sub> entre duas variáveis aleatórias ''X'' e ''Y'' com [[valor esperado|valores esperados]] &mu;<sub>''X''</sub> e &mu;<sub>''Y''</sub> e [[desvio padrão|desvios padrão]] &sigma;<sub>''X''</sub> e &sigma;<sub>''Y''</sub> é definida como:
+
O coeficiente de correlação &rho;<sub>''X, Y''</sub> entre duas variáveis aleatórias ''X'' e ''Y'' com [[valor esperado|valores esperados]] &mu;<sub>''X''</sub> e &mu;<sub>''Y''</sub> e [[desvio padrão|desvios padrão]] &sigma;<sub>''X''</sub> e &sigma;<sub>''Y''</sub> é definido como
  
−
:<tex>\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E((X-\mu_X)(Y-\mu_Y)) \over \sigma_X\sigma_Y},</tex>
+
:<tex>\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E((X-\mu_X)(Y-\mu_Y)) \over \sigma_X\sigma_Y}</tex>
  
−
:onde ''E'' é o operador [[valor esperado]] e ''cov'' significa [[covariância]].
+
onde
 +
:<tex>E</tex> é o operador [[valor esperado]] e
 +
:<tex>cov</tex> significa [[covariância]].
  
 +
Uma formulação alternativa, expressa unicamente em termos dos [[valor esperado|valores esperados]], é possível dado que
  
−
Como &mu;<sub>''X''</sub> = E(''X''),
+
:<tex>\mu_X = E(X)</tex>
−
&sigma;<sub>''X''</sub><sup>2</sup> = E(''X''<sup>2</sup>)&nbsp;&minus;&nbsp;E<sup>2</sup>(''X'') e , do mesmo modo para ''Y'', podemos escrever também
+
  
−
:<tex>\rho_{X,Y}=\frac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E^2(X)}~\sqrt{E(Y^2)-E^2(Y)}}.</tex>
+
e
  
−
A correlação é definida apenas se ambos desvios padrões são finitos e diferentes de zero. Pelo corolário da [[desigualdade de Cauchy-Schwarz]], a correlação não pode exceder 1 em [[valor absoluto]].
+
:<tex>{\sigma_X}^2 = E(X^2) - E^2(X)</tex>
  
−
==Links relevantes==
+
e que o mesmo se verifica de forma semelhante para <tex>Y</tex>, e dado também que
−
* [http://leg.ufpr.br/~silvia/CE003/node74.html Interpretação do coeficiente de correlação]
+
−
* [http://marte.dpi.inpe.br/col/sid.inpe.br/deise/1999/02.09.10.13/doc/8_135o.pdf Fusão bayesiana de imagens utilizando coeficientes de correlação] &ndash;[[PDF]]
+
−
*{{((en))}}-[http://www.mega.nu:8080/ampp/rummel/uc.htm Understanding Correlation] - Material introdutório por um professor da Universidade do Havaí.
+
−
*{{((en))}}-[http://www.vias.org/tmdatanaleng/cc_corr_coeff.html Coeficiente de correlação de Pearson] - Método de cálculo rápido
+
−
*{{((en))}}-[http://www.vias.org/simulations/simusoft_rdistri.html Learning by Simulations] - A distribuição do coeficiente de correlação
+
  
 +
:<tex>E[(X-E(X)) (Y-E(Y))] = E(XY)-E(X)E(Y)</tex>
  
−
{{Wikipedia|Correlação}}
+
temos
 +
 
 +
:<tex>\rho_{X,Y}=\frac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E^2(X)}~\sqrt{E(Y^2)-E^2(Y)}}</tex>
 +
 
 +
A correlação é definida somente se ambos os desvios padrão são finitos e diferentes de zero. Pelo corolário da [[desigualdade de Cauchy-Schwarz]], a correlação não pode exceder 1 em valor absoluto.
 +
 
 +
A correlação é 1, ou ''correlação positiva'', quando ao aumento de uma variável corresponde um aumento da outra. A correlação é -1, ou ''correlação negativa'', quando ao aumento de uma variável corresponde uma diminuição da outra. A correlação toma um valor intermédio em todos os restantes casos, indicando o grau de [[dependência linear]] entre as variáveis. Quando mais o coeficiente for aproximado de 1 ou de -1, mais forte é a correlação entre as variáveis.
 +
 
 +
Se as variáveis forem [[independência estatística|independentes]] então a correlação será 0, mas o inverso não se verifica porque o coeficiente de correlação só detecta dependências lineares entre as variáveis. Como forma de exemplo, suponha que a variável aleatória ''X'' está uniformemente distribuída pelo intervalo desde -1 até 1, e que ''Y'' = ''X''<sup>2</sup>. Então ''Y'' é completamente determinado por ''X'', de forma que ''X'' e ''Y'' são dependentes, mas a sua correlação é zero; não estão correlacionados. <!--However, in the special case when ''X'' and ''Y'' are [[bivariate Gaussian distribution|jointly normal]], uncorrelatedness is equivalent to independence. -->
 +
 
 +
Uma correlação entre duas variáveis dilui-se na presença de erros de medição causados pela estimação de uma ou de ambas as variáveis, em cujo caso a ''[[disatenuation]]'' fornece um coeficiente mais preciso.
 +
 
 +
==Referências==
 +
{{reflist}}
 +
 
 +
==Links relevantes==
 +
===Gerais===
 +
*{{link|en|2=http://jeff560.tripod.com/c.html|3=Earliest Uses: Correlation}}, primeiro usos do termo correlação e algumas referências.
 +
*{{link|en|2=http://www.thinkanddone.com/ge/Corr.html|3=Online Utility to Compute Correlation Coefficient (Scatter Diagram)}}, aplicação de cálculo do coeficiente de correlação e diagrama de dispersão
 +
*{{link|en|2=http://www.hawaii.edu/powerkills/UC.HTM|3=Understanding Correlation}}, material introdutório por um professor da Universidade do Havai.
 +
*{{link|en|2=http://www.vias.org/tmdatanaleng/cc_corr_coeff.html|3=Coeficiente de correlação de Pearson}}, método de cálculo rápido
 +
*{{link|en|2=http://www.vias.org/simulations/simusoft_rdistri.html|3=Learning by Simulations}}, a distribuição do coeficiente de correlação
 +
===Aplicados aos mercados===
 +
*[http://www.assetcorrelation.com/user/correlations/90 Matriz de correlação entre diversas classes de activos em vários períodos temporais]
  
  
 
[[Categoria:Conceitos]][[Categoria:Estatística]]
 
[[Categoria:Conceitos]][[Categoria:Estatística]]

Edição atual desde as 15h39min de 17 de agosto de 2010

<metadesc content="Na teoria das probabilidades e na estatística, correlação (frequentemente medida na forma de um coeficiente de correlação) indica a força e a direcção da relação linear entre duas variáveis aleatórias." />

Diagramas de dispersão de pontos (x, y), com o coeficiente de x e y para cada conjunto. Note que a correlação reflecte o ruído e a direcção de uma relação linear (na primeira linha), mas não a inclinação dessa relação (linha do meio), nem muitos outros aspectos das relações não-lineares (última linha). N.B.: a figura central tem uma inclinação zero mas neste caso o coeficiente de correlação é indefinido porque a variância de y é zero.

Na teoria das probabilidades e na estatística, correlação (frequentemente medida na forma de um coeficiente de correlação) indica a força e a direcção da relação linear entre duas variáveis aleatórias. Esta definição difere do uso normal do termo correlação, que se refere a qualquer relação, não necessariamente linear.

No uso geral em estatística, correlação refere-se à medida em que duas variáveis aleatórias se afastam da independência estatística. Neste sentido geral, existem vários coeficientes para medir o grau de correlação, adaptados à natureza dos dados.

Coeficiente produto-momento de Pearson

Vários coeficientes são utilizados para situações diferentes. O mais conhecido é o coeficiente de correlação de Pearson, o qual é obtido dividindo a covariância de duas variáveis pelo produto dos seus desvios padrão. Apesar do nome, ela foi inicialmente apresentada por Francis Galton<ref name="13ways"> Rodgers, J. L.; Nicewander, W. A. (1988). "Thirteen ways to look at the correlation coefficient" (em inglês). The American Statistician 42: 59–66. DOI:10.2307/2685263.  </ref>.

Propriedades matemáticas

O coeficiente de correlação ρX, Y entre duas variáveis aleatórias X e Y com valores esperados μX e μY e desvios padrão σX e σY é definido como

\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E((X-\mu_X)(Y-\mu_Y)) \over \sigma_X\sigma_Y}

onde

E é o operador valor esperado e
cov significa covariância.

Uma formulação alternativa, expressa unicamente em termos dos valores esperados, é possível dado que

\mu_X = E(X)

e

{\sigma_X}^2 = E(X^2) - E^2(X)

e que o mesmo se verifica de forma semelhante para Y, e dado também que

E[(X-E(X)) (Y-E(Y))] = E(XY)-E(X)E(Y)

temos

\rho_{X,Y}=\frac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E^2(X)}~\sqrt{E(Y^2)-E^2(Y)}}

A correlação é definida somente se ambos os desvios padrão são finitos e diferentes de zero. Pelo corolário da desigualdade de Cauchy-Schwarz, a correlação não pode exceder 1 em valor absoluto.

A correlação é 1, ou correlação positiva, quando ao aumento de uma variável corresponde um aumento da outra. A correlação é -1, ou correlação negativa, quando ao aumento de uma variável corresponde uma diminuição da outra. A correlação toma um valor intermédio em todos os restantes casos, indicando o grau de dependência linear entre as variáveis. Quando mais o coeficiente for aproximado de 1 ou de -1, mais forte é a correlação entre as variáveis.

Se as variáveis forem independentes então a correlação será 0, mas o inverso não se verifica porque o coeficiente de correlação só detecta dependências lineares entre as variáveis. Como forma de exemplo, suponha que a variável aleatória X está uniformemente distribuída pelo intervalo desde -1 até 1, e que Y = X2. Então Y é completamente determinado por X, de forma que X e Y são dependentes, mas a sua correlação é zero; não estão correlacionados.

Uma correlação entre duas variáveis dilui-se na presença de erros de medição causados pela estimação de uma ou de ambas as variáveis, em cujo caso a disatenuation fornece um coeficiente mais preciso.

Referências

<references />

Links relevantes

Gerais

Aplicados aos mercados

Obtida de "https://www.thinkfnwiki.com/wiki/index.php?title=Correlação&oldid=48948"