Diferenças entre edições de "Delta de Dirac"
(Categoria Distribuições Estatísticas) |
|||
| (3 edições intermédias não estão a ser mostradas.) | |||
| Linha 1: | Linha 1: | ||
| − | [[Imagem:Dirac distribution PDF.png|thumb|A distribuição delta de Dirac.]] | + | [[Imagem:Dirac distribution PDF.png|thumb|A distribuição delta de Dirac.]] |
| − | A '''Delta de Dirac''' ou, como costuma ser impropriamente chamada, a '''função Delta de Dirac''', introduzida por | + | A '''Delta de Dirac''' ou, como costuma ser impropriamente chamada, a '''função Delta de Dirac''', introduzida por Paul Dirac, é uma função nula em todo o seu domínio excepto em ''x'' = 0, ponto no qual é infinito . Esta função é normalmente representada por δ(x) e o análogo desta função no domínio discreto é o Delta de Kronecker. <!-- corrigir isto: isto já eh matemática demasiado abstracta-->Note-se que o '''Delta de Dirac''' não é uma função mas sim uma [[distribuição]]. |
== Definição == | == Definição == | ||
| − | : <tex>\delta(x) = \begin{cases} \infty, & x = 0 \\ 0, & x \ne 0 \end{cases}</tex> | + | :<tex>\delta(x) = \begin{cases} \infty, & x = 0 \\ 0, & x \ne 0 \end{cases}</tex> |
| − | + | ||
| − | + | ||
| + | :<tex>\int_{-\infty}^{\infty} \delta(x) dx = 1\,</tex> | ||
A '''Delta de Dirac''' possui a seguinte propriedade: | A '''Delta de Dirac''' possui a seguinte propriedade: | ||
| − | <tex>\int\delta(x-x^\prime)f(x)dx = f(x^\prime)\,</tex> | + | |
| + | :<tex>\int\delta(x-x^\prime)f(x)dx = f(x^\prime)\,</tex> | ||
| + | |||
== Aplicação em Física == | == Aplicação em Física == | ||
| − | Em | + | Em física, ela é usada para representar densidades de objectos pontuais (ex. carga pontual) |
== Aplicação em Estatística == | == Aplicação em Estatística == | ||
| Linha 21: | Linha 22: | ||
O [[valor esperado]] de uma variável aleatória contínua é escrito como: | O [[valor esperado]] de uma variável aleatória contínua é escrito como: | ||
| + | |||
* <tex>E[X] = \int x f(x) dx\,</tex> | * <tex>E[X] = \int x f(x) dx\,</tex> | ||
| + | |||
Por outro lado, o valor esperado de uma variável aleatória discreta é escrito como: | Por outro lado, o valor esperado de uma variável aleatória discreta é escrito como: | ||
| + | |||
* <tex>E[X] = \sum x_i p(x_i)\,</tex> | * <tex>E[X] = \sum x_i p(x_i)\,</tex> | ||
| + | |||
O uso da '''Delta de Dirac''' permite unificar estas duas fórmulas, definindo-se a [[função densidade de probabilidade]] de uma variável aleatória contínua por: | O uso da '''Delta de Dirac''' permite unificar estas duas fórmulas, definindo-se a [[função densidade de probabilidade]] de uma variável aleatória contínua por: | ||
| + | |||
* <tex>f(x) = \sum p(x_i) \delta(x - x_i)\,</tex> | * <tex>f(x) = \sum p(x_i) \delta(x - x_i)\,</tex> | ||
| + | |||
== Integral == | == Integral == | ||
| − | Em certo sentido, pode-se dizer que a '''delta de Dirac''' é a derivada da | + | Em certo sentido, pode-se dizer que a '''delta de Dirac''' é a derivada da função de passo Heaviside, ou que a integral da '''delta de Dirac''' é a função de passo Heaviside: |
| + | |||
:<tex> H(x) = \int_{-\infty}^x { \delta(t)} \mathrm{d}t </tex> | :<tex> H(x) = \int_{-\infty}^x { \delta(t)} \mathrm{d}t </tex> | ||
| Linha 37: | Linha 45: | ||
Física matemática, Eugene Butkov, ed. Campus 1995 | Física matemática, Eugene Butkov, ed. Campus 1995 | ||
| − | |||
| − | |||
| − | {{Wikipedia| | + | {{Wikipedia|Delta de Dirac}} |
| + | |||
| + | [[categoria:Distribuições]] | ||
| + | [[Categoria:Estatística]] | ||
Edição atual desde as 12h13min de 7 de novembro de 2008
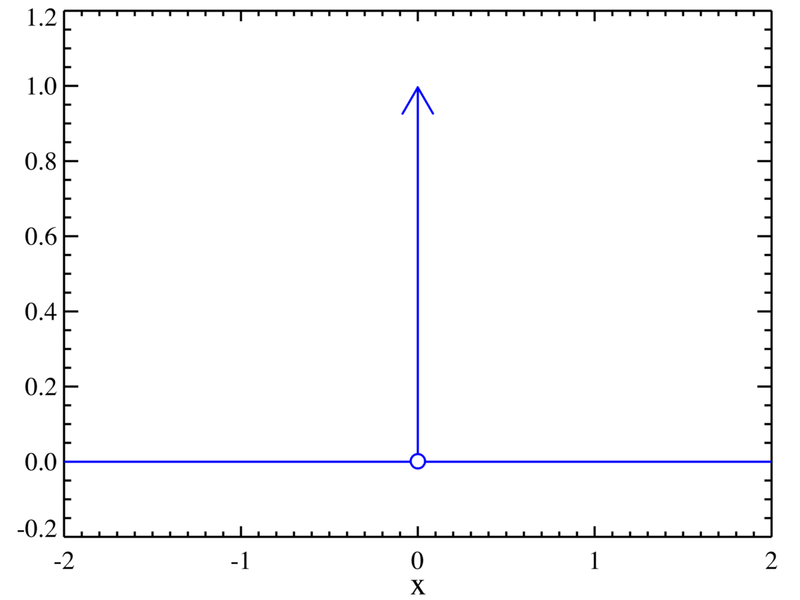A Delta de Dirac ou, como costuma ser impropriamente chamada, a função Delta de Dirac, introduzida por Paul Dirac, é uma função nula em todo o seu domínio excepto em x = 0, ponto no qual é infinito . Esta função é normalmente representada por δ(x) e o análogo desta função no domínio discreto é o Delta de Kronecker. Note-se que o Delta de Dirac não é uma função mas sim uma distribuição.
Definição
A Delta de Dirac possui a seguinte propriedade:
Aplicação em Física
Em física, ela é usada para representar densidades de objectos pontuais (ex. carga pontual)
Aplicação em Estatística
Em estatística, ela permite generalizar as fórmulas para variáveis aleatórias discretas e contínuas, por exemplo:
O valor esperado de uma variável aleatória contínua é escrito como:
Por outro lado, o valor esperado de uma variável aleatória discreta é escrito como:
O uso da Delta de Dirac permite unificar estas duas fórmulas, definindo-se a função densidade de probabilidade de uma variável aleatória contínua por:
Integral
Em certo sentido, pode-se dizer que a delta de Dirac é a derivada da função de passo Heaviside, ou que a integral da delta de Dirac é a função de passo Heaviside:
Referências
Física matemática, Eugene Butkov, ed. Campus 1995
|
Esta página usa conteúdo da Wikipedia. O artigo original estava em Delta de Dirac. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License. |
