Kriging

Kriging, também muitas vezes traduzido como Krigagem, é um método de regressão usado em geoestatística para aproximar ou interpolar dados. A teoria de Kriging foi desenvolvida a partir dos trabalhos do seu inventor, Daniel G. Krige, pelo matemático francês Georges Matheron, no começo dos anos sessenta. Na comunidade estatística, também é conhecido como “Processo Gaussiano de Regressão”. A estimação com base em apenas um atributo insere-se no âmbito da Kriging; a estimação de um atributo à custa de outros atributos insere-se no âmbito da Cokriging.

Introdução

Kriging pode ser entendido como uma predição linear ou uma forma da Inferência bayesiana. Parte do princípio que pontos próximos no espaço tendem a ter valores mais parecidos do que pontos mais afastados. A técnica de Kriging assume que os dados recolhidos de uma determinada população se encontram correlacionados no espaço. Isto é, se num aterro de resíduos tóxicos e perigosos a concentração de Zinco num ponto p é x, é muito provável que se encontrem resultados muito próximos de x quanto mais próximos se estiver do ponto p (princípio da geoestatística). Porém, a partir de determinada distância de p, certamente não se encontrarão valores aproximados de x porque a correlação espacial pode deixar de existir.

Considera-se o método de Kriging do tipo BLUE (Best Linear Unbiased Estimator - Melhor Estimador Linear não-Viciado): é linear porque as suas estimativas são combinações lineares ponderadas dos dados existentes; é não enviezada pois procura que a média dos erros (desvios entre o valor real e o valor estimado) seja nula; é a melhor porque os erros de estimação apresentam uma variância (variância de estimação) mínima. O termo Kriging abrange um conjunto de métodos, sendo os mais usuais os seguintes:

Tipos de Kriging

Kriging Simples

Assume que as médias locais são relativamente constantes e de valor muito semelhante à média da população que é conhecida. A média da população é utilizada para cada estimação local, em conjunto com os pontos vizinhos estabelecidos como necessários para a estimação.

Kriging Ordinário

As médias locais não são necessáriamente próximas da média da população usando-se apenas os pontos vizinhos para a estimação. É o método mais usado em problemas ambientais.

Cokriging

É uma extensão do anterior a situações em que duas ou mais variáveis são espacialmente dependentes e a variável que se quer estimar não está amostrada com a intensidade com que estão as outras variáveis dependentes, utilizando-se os valores destas e as suas dependências para estimar a variável requerida.

Conceitos matemáticos

O Método de Kriging utiliza-se de diversas teorias explanadas na estatística. No entanto, para deixarmos mais claras as teorias de estatística usadas e mais direcionadas ao escopo deste texto, explicaremos alguns conceitos.

Semi-variância e semi-variograma

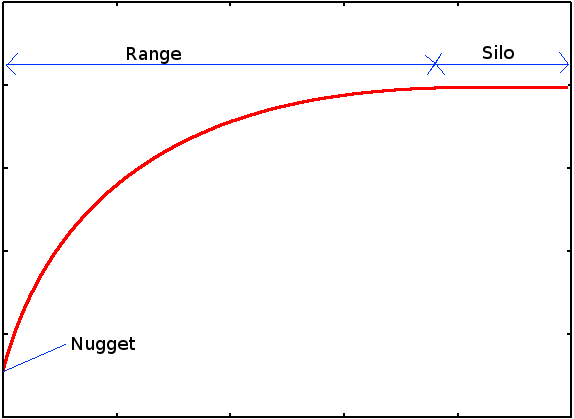A semi-variância é a medida do grau de dependência espacial entre duas amostras. A magnitude da semi-variância entre dois pontos depende da distância entre eles, implicando em semi-variâncias menores para distâncias menores e semi-variâncias maiores para distâncias maiores. O gráfico das semi-variâncias em função da distância a um ponto é chamado de Semi-variograma. A partir de uma certa distância a semi-variância não mais aumentará com a distância e se estabilizará num valor igual à variância média, dando a esta região o nome de silo (sill). A distância entre o início do semi-variograma e o começo do silo recebe o nome de range. Ao extrapolarmos a curva do semi-variograma para a distância zero, podemos chegar a um valor não-nulo de semi-variância. Este valor recebe o nome de Efeito Pepita (Nugget Effect).

Modelos de Variograma

No Método de Kriging normalmente são usados quatro tipos de variogramas. Neles, são usadas as seguintes variáveis:

: variância

: nugget

: silo

: variância assintótica

: distância de separação

Linear

Este modelo não apresenta silo e é muito simples. Sua curva pode ser representada por:

Esférico

A forma esférica é a mais utilizada e possui silo. Sua forma é definida por:

Exponencial

A curva do variograma exponencial respeita a seguinte equação:

Gaussiano

A forma gaussiana é dada por:

O Método de Kriging

Determinação do Semivariograma

Toma-se como base a simulação de um sistema de duas dimensões (2D) que contém um número finito de pontos onde é possível a medição de uma grandeza qualquer. Após a adquisição destes dados, iniciar-se-á a interpolação por Kriging buscando alcançar uma maior resolução. O primeiro passo é construir um semivariograma experimental. Para tal, calcula-se a semivariância de cada ponto em relação aos demais e insere-se no gráfico da semivariância pela distância.

A partir deste gráfico estima-se o modelo de variograma que melhor se aproxima da curva obtida. O efeito pepita pode estar presente no semivariograma experimental e deve ser considerado. Determinado o modelo do semivariograma a ser usado, inicia-se a fase de cálculos. Sendo o semivariograma uma função que depende da direção, é natural que apresente valores diferentes conforme a direção, recebendo este fenômeno o nome de Anisotropia. Caso o semivariograma apresente uma forma semelhante em todas as direções do espaço, só dependendo de h, diz-se que a estrutura é Isotrópica, i. e., sem direções privilegiadas de variabilidade.

Cálculo dos Pesos

Considere, para o cálculo do Kriging, a seguinte fórmula:

onde é o número de amostras obtidas, é o valor obtido no ponto e é o peso designado ao ponto . A fim de obter os pesos de cada um dos pontos, para cada um deles é realizado um cálculo de . Tal procedimento depende do tipo de Kriging que está sendo utilizado. Salienta-se a seguinte notação:

: peso do j-ésimo ponto

: valor da semi-variância de

: variável temporária

Kriging Ordinário

Neste caso é utilizado a média local dos pontos amostrados. Por conseguinte, deve-se normalizar a média dos pesos. Consequentemente, tem-se um resultado mais preciso do que o Kriging Simples. Utilizar-se-ão as seguintes equações para a determinação dos valores dos pesos no p-ésimo ponto:

Kriging Simples

Para este caso, utiliza-se a média de todos os dados. Implica-se, portanto, em não se normalizar a média local dos pesos, como no caso anterior. Assim, teremos quase que a mesma equação, exceto pela exclusão de e pela última equação. A característica principal deste método é a geração de gráficos mais lisos e mais esteticamente suaves. Deve-se salientar que este caso é menos preciso que o caso anterior. Os valores dos pesos para o p-ésimo ponto serão dados por:

Obtendo o Ponto Interpolado

Ao obtermos os valores de , calcula-se o valor de :

Desta maneira, calcula-se o valor interpolado para todos os pontos desejados. Ressalta-se que somente devem ser utilizados os valores adquiridos acima.

Interpolando Outros Pontos

A obtenção do valor interpolado em um outro ponto requer a repetição de todos os cálculos realizados a partir da obtenção do modelo de variograma. Desta forma, para aumentarmos a resolução que é pretendida, deve-se recorrer à métodos matemáticos para a resolução computacional. Diversos códigos foram desenvolvidos para esta resolução, mas um dos melhores algoritmos pode ser obtido no link abaixo. Ele fora desenvolvido inicialmente para a linguagem Fortran, porém ele foi recodificado para C com a ajuda da biblioteca fortran2c e se apresenta totalmente em C:

• Kriging Interpolation Algorithm in C

Links relevantes

• SPRING - Geoestatística - Krigeagem
• Modelos de Dados Geográficos
• Kriging(ems-i)

Esta página usa conteúdo da Wikipedia. O artigo original estava em Kriging. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License.