Paradoxo do aniversário

Da Thinkfn

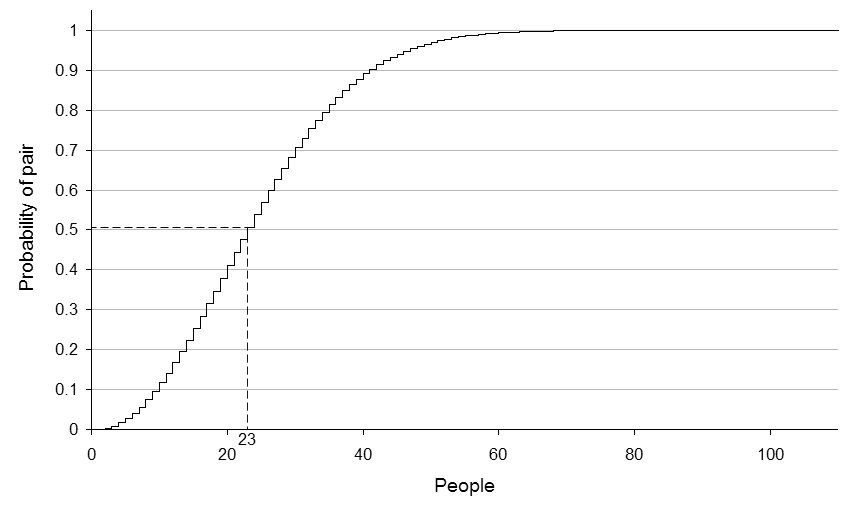Um gráfico mostrando a probabilidade de que pelo menos duas pessoas tenham a mesma data de aniversário em um certo número de pessoas. A aparência de escada deve-se ao eixo x que é tomado apenas de valores inteiros, visto que indica o número de pessoas. Em teoria das probabilidades, o paradoxo do aniversário afirma que dado um grupo de 23 (ou mais) pessoas escolhidas aleatoriamente, a chance de que duas pessoas terão o mesma data de aniversário é de mais de 50%. Para 57 ou mais pessoas, a probabilidade é maior do que 99%, entretanto, ela não pode ser exatamente 100% exceto que se tenha pelo menos 366 pessoas. Calcular essa probabilidade (e as relacionas a ela) é o problema do aniversário.

Calculando a probabilidade

Para calcular aproximadamente a probabilidade de que em uma sala com n pessoas, pelo menos duas possuam o mesmo aniversário, desprezamos variações na distribuição, tais como anos bissextos, gêmeos, variações sazonais ou semanais, e assumimos que 365 possíveis aniversários são todos igualmente prováveis. Distribuições de aniversários na realidade não são uniforme uma vez que as datas não são equiprováveis.<ref>Em particular, muitas crianças nascem no verão, especialmente nos meses de Julho, Agosto e Setembro (para o hemisfério norte) [1]; ainda assim, em ambientes como salas de aula onde muitas pessoas partilham a mesma data de aniversário, isso torna-se relevante devido a maneira em que o hospital trabalha, onde partos induzidos ou realizados por cesarianas geralmente não são marcados nos finais de semana, mais crianças nascem na segunda e terça-feira do que nos finais de semana. Ambos fatores tendem a ampliar as chances de aniversários idênticos, visto que um subconjunto mais denso possuem mais pares possíveis</ref>

É mais fácil calcular a probabilidade p(n) do que todos os n aniversários diferentes. Se n > 365, pelo Princípio da Casa dos Pombos esta probabilidade é 0. Por outro lado, se n ≤ 365, ele é dado por


\bar p(n) = 1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) = { 365 \cdot 364 \cdots (365-n+1) \over 365^n } = { 365! \over 365^n (365-n)!}


porque a segunda pessoa não pode ter o mesmo aniversário do que o primeiro (364/365), o terceiro não pode ter o mesmo aniversário do que o segundo (363/365), etc.

O evento de pelo menos duas pessoas entre n terem o mesmo aniversário é o complementar de todos n serem diferentes. Consequentemente, sua probabilidade p(n) é


p(n) = 1 - \bar p(n) .


Esta probabilidade ultrapassa 1/2 para n = 23 (com valor aproximado de 50.7%). A seguinte tabela mostra a probabilidade para alguns valores de n (ignorando anos bissextos como descrito anteriormente):

n p(n)
10 12%
20 41%
23 50.7%
30 70%
50 97%
100 99.99996%
200 99.9999999999999999999999999998%
300 (1 − 7×10−73) × 100%
350 (1 − 3×10−131) × 100%
366 100%

Aproximações

Utilizando a expansão da série de Taylor para a função exponencial


e^x = 1 + x + \frac{x^2}{2!}+\cdots


Um gráfico mostrando precisão da aproximação 1 − exp(−n2/(2⋅365)). a primeira expressão derivada para p(n) pode ser aproximado a


\bar p(n) \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365}


= 1 \cdot e^{-(1+2+ \cdots +(n-1))/365}


= e^{-(n(n-1))/2 \cdot 365}


Então,


p(n) = 1-\bar p(n) \approx 1 - e^{-(n(n-1))/2 \cdot 365}


Uma outra aproximação a grosso modo é dada por


p(n)\approx 1-e^{-n^2/{2 \cdot 365}},\,


que, como ilustrado pelo gráfico, ainda possui uma boa precisão.

Aproximação de Poisson

Utilizando a aproximação de Poisson para a binomial,


\mathrm{Poi}\left(\frac{C(23, 2)}{365}\right) \approx \mathrm{Poi}\left(\frac{253}{365}\right) \approx \mathrm{Poi}(0.6932)


\Pr(X>0)=1-\Pr(X=0)=1-e^{-0.6932}=1-0.499998=0.500002.


Novamente, ela é maior que 50%.

Referências

  • Zoe Emily Schnabel: "The estimation of the total fish population of a lake", American Mathematical Monthly 45 (1938), pages 348-352
  • M. Klamkin and D. Newman: "Extensions of the birthday surprise", Journal of Combinatorial Theory 3 (1967), pages 279-282.
  • D. Bloom: "A birthday problem", American Mathematical Monthly 80 (1973), pages 1141-1142. This problem solution contains a proof that the probability of two matching birthdays is least for a uniform distribution of birthdays.

Notas

<references />

Links relevantes


Smallwikipedialogo.png

Esta página usa conteúdo da Wikipedia. O artigo original estava em Paradoxo do aniversário. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License.

Obtida de "https://www.thinkfnwiki.com/wiki/index.php?title=Paradoxo_do_aniversário&oldid=16176"