Distribuição de Poisson
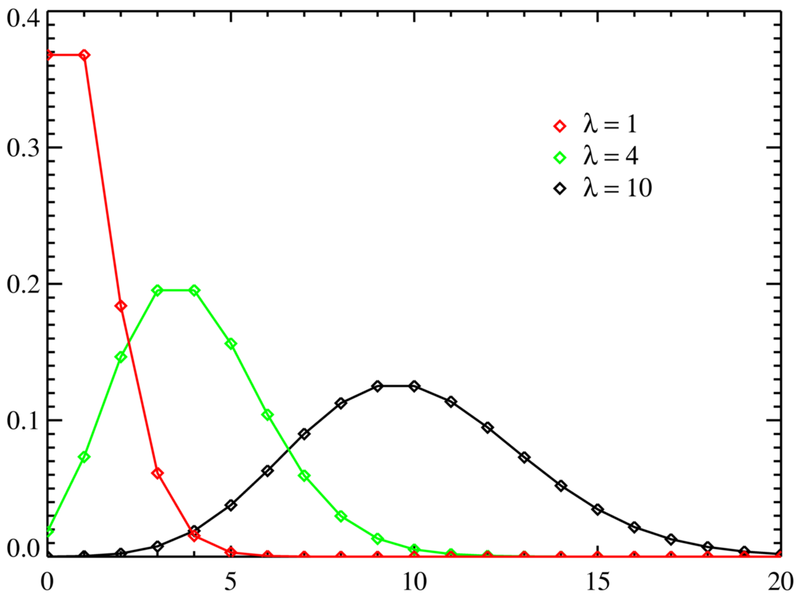Na teoria da probabilidade e na estatística, a distribuição de Poisson é uma distribuição de probabilidade discreta. Ela expressa, por exemplo, a probabilidade de um certo número de eventos ocorrerem num dado período tempo, caso estes ocorram com uma taxa média conhecida e caso cada evento seja independente do tempo decorrido desde o último evento. A distribuição foi descoberta por Siméon-Denis Poisson (1781–1840) e publicada, conjuntamente com a sua teoria da probabilidade, em 1838 no seu trabalho Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Inquérito sobre a probabilidade em julgamentos sobre matérias criminais e civis"). O trabalho focava-se em certas variáveis aleatórias N que contavam, entre outras coisas, o número de ocorrências discretas (por vezes chamadas de "chegadas") que tinham lugar durante um intervalo de tempo de determinado comprimento. A probabilidade de que existam exactamente k ocorrências (k sendo um inteiro não negativo, k = 0, 1, 2, ...) é
além disso:
onde
- e é base do logaritmo natural (e = 2.71828...),
- k! é o factorial de k,
- λ é um número real, igual ao número esperado de ocorrências que ocorrem num dado intervalo de tempo. Por exemplo, se o evento ocorre a uma média de 4 minutos, e estamos interessados no número de eventos que ocorrem num intervalo de 10 minutos, usariámos como modelo a distribuição de Poisson com λ = 10/4 = 2.5.
Como função de k, esta é a função massa de probabilidade. A distribuição de Poisson pode ser derivada como um caso limite da distribuição binomial.
|
Esta página usa conteúdo da Wikipedia. O artigo original estava em Distribuição de Poisson. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License. |
